Đề Thi Thử Môn Toán THPT 2025 - Đề Số 13 - VuaDeThi.com

Trắc nghiệm trả lời ngắn

Câu 5. Người ta thiết kế một mẫu gạch lát nền nhà có dạng hình vuông, cạnh 4 dm. Bốn góc viên gạch màu trắng, phần ở giữa màu xanh (như hình vẽ). Đường viền của phần màu xanh bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kỳ thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng 2 dm22\,dm^{2}. Hãy cho biết phần màu xanh có diện tích bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?

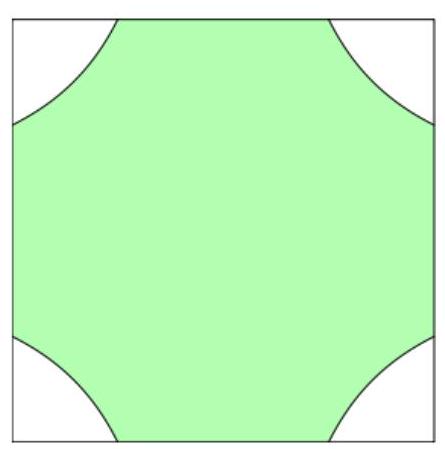
Hình minh họa

xem đáp án bên dưới

Đáp án

13,5

Gắn trục tọa độ OxyO x y vào viên gạch sao cho hai trục trùng với hai đường đối xứng, gốc OO ở tâm hình vuông như hình dưới.

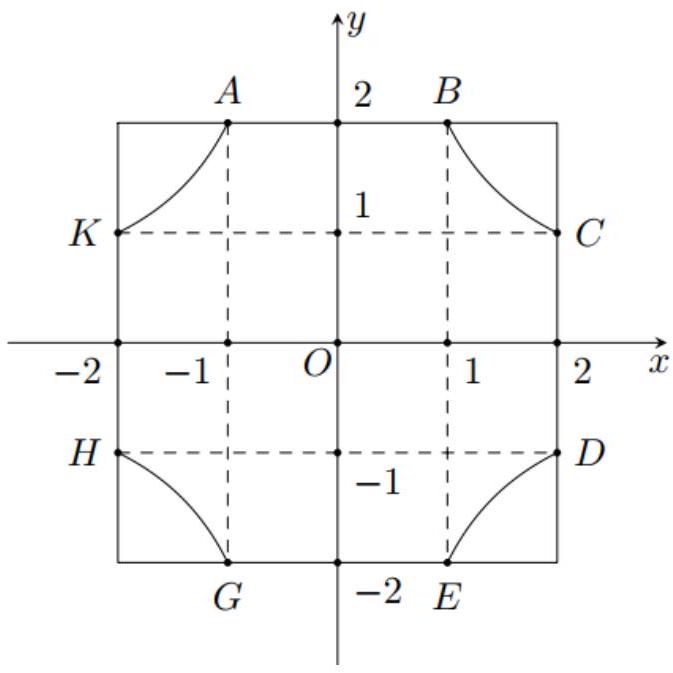
Giả sử toạ độ một điểm trên đường viền cong là (x;y)(x ; y). Theo giả thiết, ta có: ∣xy∣=2|x y|=2. Suy ra y=2xy=\frac{2}{x} hoặc y=−2xy=-\frac{2}{x}. Ứng với hình trên, ta có các đường viền cong AK,DEA K, D E là một phần của đồ thị hàm số y=−2xy=-\frac{2}{x}; các đường viền cong BC,GHB C, G H là một phần của đồ thị hàm số y=2xy=\frac{2}{x}.

Khi đó, diện tích phần màu xanh bằng:

∫−2−1∣−2x−2x∣dx+∫12∣2x−−2x∣dx+SABEG=∫−2−1(−2x−2x)dx+∫12(2x−−2x)dx+4⋅2=−4ln⁡∣x∣∥−2−1+4ln⁡∣x∥12+8≈13,5(dm2).\begin{aligned} & \int_{-2}^{-1}\left|\frac{-2}{x}-\frac{2}{x}\right| \mathrm{d} x+\int_{1}^{2}\left|\frac{2}{x}-\frac{-2}{x}\right| \mathrm{d} x+S_{A B E G}=\int_{-2}^{-1}\left(-\frac{2}{x}-\frac{2}{x}\right) \mathrm{d} x+\int_{1}^{2}\left(\frac{2}{x}-\frac{-2}{x}\right) \mathrm{d} x+4 \cdot 2 \\ & =-4 \ln |x|\left\|_{-2}^{-1}+4 \ln \mid x\right\|_{1}^{2}+8 \approx 13,5\left(\mathrm{dm}^{2}\right) . \end{aligned}