PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12 .

Mỗi câu hỏi thí sinh chỉ chọn một phương án.

Câu 1. Phát biểu nào sau đây là đúng?

A. ∫(sin⁡x+cos⁡x)dx=∫sin⁡x dx+∫cos⁡xdx\int(\sin x+\cos x) \mathrm{d} x=\int \sin x \mathrm{~d} x+\int \cos x \mathrm{d} x.

B. ∫(sin⁡x+cos⁡x)dx=∫sin⁡x dx−∫cos⁡xdx\int(\sin x+\cos x) \mathrm{d} x=\int \sin x \mathrm{~d} x-\int \cos x \mathrm{d} x.

C. ∫(sin⁡x+cos⁡x)dx=−∫sin⁡x dx+∫cos⁡xdx\int(\sin x+\cos x) \mathrm{d} x=-\int \sin x \mathrm{~d} x+\int \cos x \mathrm{d} x.

D. ∫(sin⁡x+cos⁡x)dx=−∫sin⁡x dx−∫cos⁡xdx\int(\sin x+\cos x) \mathrm{d} x=-\int \sin x \mathrm{~d} x-\int \cos x \mathrm{d} x.

chi tiết

Câu 2. Tọa độ của vectơ u⃗=k⃗+2j⃗\vec{u}=\vec{k}+2 \vec{j} là:

A. (1;0;2)(1 ; 0 ; 2).

B. (2;0;1)(2 ; 0 ; 1).

C. (0;2;1)(0 ; 2 ; 1).

D. (1;2;0)(1 ; 2 ; 0).

chi tiết

Câu 3. Tập xác định của hàm số y=2x−3+4x+5y=2x-3+\frac{4}{x+5} là:

A. R\{3}R \backslash\{3\}.

B. R\{−3}R \backslash\{-3\}.

C. R\{5}R \backslash\{5\}.

D. R\{−5}R \backslash\{-5\}.

chi tiết

Câu 4. Giá trị lớn nhất của hàm số y=cos⁡xy=\cos x là:

A. 1 .

B. -1 .

C. π\pi.

D. 2π2 \pi.

chi tiết

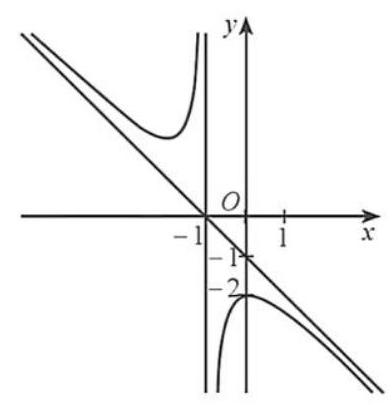
Câu 5. Nếu hàm số y=f(x)y=f(x) thỏa mãn lim⁡x→−∞f(x)=−1;lim⁡x→+∞f(x)=1\lim_{x\rightarrow-\infty} f(x)=-1 ; \lim_{x\rightarrow+\infty} f(x)=1 thì:

A. Đồ thị hàm số có 2 tiệm cận đứng là x=−1x=-1 và x=1x=1.

B. Đồ thị hàm số có 1 tiệm cận đứng là x=−1x=-1 và 1 tiệm cận ngang là y=1y=1.

C. Đồ thị hàm số có 1 tiệm cận ngang là y=−1y=-1 và 1 tiệm cận đứng là x=1x=1.

D. Đồ thị hàm số có 2 tiệm cận ngang là y=−1y=-1 và y=1y=1.

chi tiết

Câu 6. Trong không gian với hệ trục tọa độ Oxy zOxy\,z, mặt phẳng (P):3x−y+5=0(P): 3x-y+5=0 có một vectơ pháp tuyến là:

A. n⃗1=(3;−1;5)\vec{n}_{1}=(3 ;-1 ; 5).

B. n⃗2=(3;−1;0)\vec{n}_{2}=(3 ;-1 ; 0).

C. n⃗3=(3;1;5)\vec{n}_{3}=(3 ; 1 ; 5).

D. n⃗4=(3;−1)\vec{n}_{4}=(3 ;-1).

chi tiết

Câu 7. Hàm số nào sau đây là một nguyên hàm của hàm số f(x)=1xln⁡5f(x)=\frac{1}{x\ln 5} ?

A. y=ln⁡xy=\ln x.

B. y=ln⁡(5x)y=\ln (5x).

C. y=log⁡5xy=\log_{5} x.

D. y=ln⁡x5y=\ln \frac{x}{5}.

chi tiết

Câu 8. Trong không gian với hệ tọa độ Oxy zOxy\,z, mặt cầu có tâm I(3;2;−1)I(3 ; 2 ;-1) và bán kính 4 có phương trình là:

A. (x−3)2+(y−2)2+(z+1)2=2(x-3)^2+(y-2)^2+(z+1)^2=2.

B. (x−3)2+(y−2)2+(z+1)2=16(x-3)^2+(y-2)^2+(z+1)^2=16.

C. (x−3)2+(y−2)2+(z−1)2=16(x-3)^2+(y-2)^2+(z-1)^2=16.

D. (x+3)2+(y+2)2+(z−1)2=16(x+3)^2+(y+2)^2+(z-1)^2=16.

chi tiết

Câu 9. Trong không gian với hệ trục tọa độ Oxy zOxy\,z, khoảng cách từ điểm M(1;−2;0)M(1 ;-2 ; 0) đến mặt phẳng (P):x−2y+2z+4=0(P): x-2y+2z+4=0 là:

A. 1 .

B. 9 .

C. 3 .

D. 5 .

chi tiết

Câu 10. Khi thống kê chiều cao (đơn vị: centimét) của học sinh lớp 12 A, người ta thu được mẫu số liệu ghép nhóm như bảng sau:

Nhóm[155;160)[155 ; 160)[160;165)[160 ; 165)[165;170)[165 ; 170)[170;175)[170 ; 175)[175;180)[175 ; 180)
Tần số232492n=40n=40

Khoảng biến thiên của mẫu số liệu ghép nhóm đó bằng:

A. 180 cm .

B. 24 cm .

C. 22 cm .

D. 25 cm .

chi tiết

Câu 11. Cho AA và BB là hai biến cố độc lập thỏa mãn P(A)=0,4P(A)=0,4 và P(B)=0,2P(B)=0,2. Khi đó, P(A∩B)P(A \cap B) bằng:

A. 0,6.

B. 0,2 .

C. 0,08 .

D. 0,8 .

chi tiết

Câu 12. Hàm số nào sau đây có đồ thị là đường cong như bên?

Hình minh họa

A. y=x2+2x+2−x−1y=\frac{x^{2}+2x+2}{-x-1}.

B. y=x2+2x+2x+1y=\frac{x^{2}+2x+2}{x+1}.

C. y=x2−2x+2x−1y=\frac{x^{2}-2x+2}{x-1}.

D. y=x2−2x+2x+1y=\frac{x^{2}-2x+2}{x+1}.

chi tiết

PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4.

Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.

Câu 1. Cho hàm số y=f(x)y=f(x) có đạo hàm trên RR và đồ thị như hình bên.

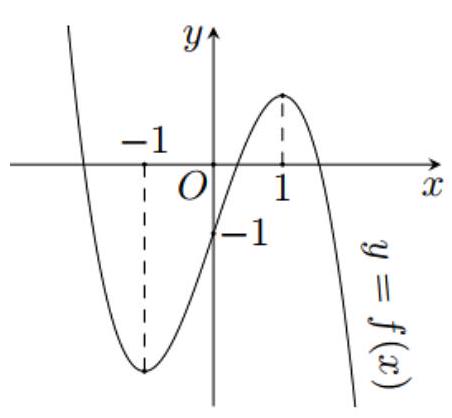
Hình minh họa

a) Hàm số nghịch biến trên khoảng (−∞;−1)(-\infty ;-1).

b) Hàm số đạt cực tiểu tại điểm x0=−1x_{0}=-1.

c) Đạo hàm của hàm số nhận giá trị không âm trên khoảng (−1;1)(-1 ; 1).

d) Giá trị lớn nhất của hàm số trên đoạn [−1;0][-1 ; 0] bằng 1 .

chi tiết

Câu 2. Vào năm 2014, dân số nước ta khoảng 90,7 triệu người. Giả sử, dân số nước ta sau tt năm được xác định bởi hàm số S(t)S(t) (đơn vị: triệu người), trong đó tốc độ gia tăng dân số được cho bởi S′(t)=1,2698e0,014tS^{\prime}(t)=1,2698e^{0,014t}, với tt là số năm kể từ năm 2014, S′(t)S^{\prime}(t) tính bằng triệu người/năm.

a) S(t)S(t) là một nguyên hàm của S′(t)S^{\prime}(t).

b) S(t)=90,7e0,014t+90,7S(t)=90,7e^{0,014t}+90,7.

c) Theo công thức trên, tốc độ tăng dân số nước ta năm 2034 (làm tròn đến hàng phần mười của triệu người/năm) khoảng 1, 7 triệu người/năm.

d) Theo công thức trên, dân số nước ta năm 2034 (làm tròn đến hàng đơn vị của triệu người) khoảng 120 triệu người.

chi tiết

Câu 3. Trong không gian Oxy zOxy\,z, cho hình chóp S.ABCDS . ABCD có S(0;0;3,5)S(0 ; 0 ; 3,5), ABCDABCD là hình chữ nhật với A(0;0;0)A(0 ; 0 ; 0), B(4;0;0)B(4 ; 0 ; 0), D(0;10;0)D(0 ; 10 ; 0) (tham khảo hình bên).

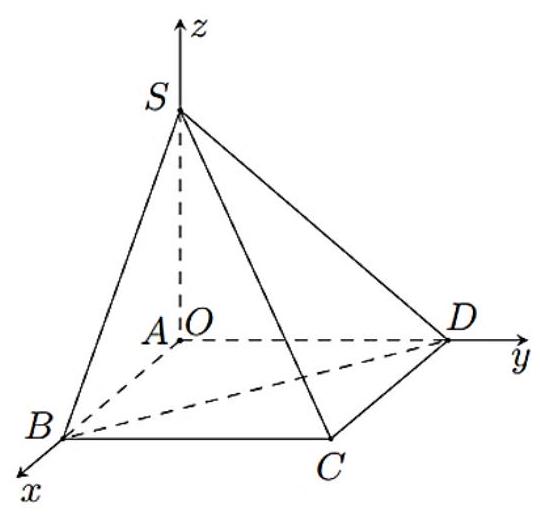
Hình minh họa

a) Tọa độ điểm C(4;10;0)C(4 ; 10 ; 0).

b) Phương trình mặt phẳng (SBD)(SBD) là x4+y10−z3,5=1\frac{x}{4}+\frac{y}{10}-\frac{z}{3,5}=1.

c) Tọa độ của vectơ SC→\overrightarrow{SC} là (4;10;−3,5)(4 ; 10 ;-3,5).

d) Góc giữa đường thẳng SCSC và mặt phẳng (SBD)(SBD) (làm tròn đến hàng đơn vị của độ) là 20∘20^{\circ}.

chi tiết

Câu 4. Khi điều tra sức khỏe nhiều người cao tuổi ở một địa phương, người ta thấy rằng có 40%40\% người cao tuổi bị bệnh tiểu đường. Bên cạnh đó, số người bị bệnh huyết áp cao trong những người bị bệnh tiểu đường là 70%70\%, trong những người không bị bệnh tiểu đường là 25%25\%. Chọn ngẫu nhiên 1 người cao tuổi để kiểm tra sức khỏe.

a) Xác suất chọn được người bị bệnh tiểu đường là 0,4 .

b) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó bị bệnh tiểu đường, là 0,7 .

c) Xác suất chọn được người bị bệnh huyết áp cao, biết người đó không bị bệnh tiểu đường, là 0,75.

d) Xác suất chọn được người bị bệnh huyết áp cao là 0,8 .

chi tiết

PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .

Câu 1. Cho hình lăng trụ đều ABC⋅A′B′C′ABC \cdot A'B'C'. Biết khoảng cách từ điểm CC đến mặt phẳng (ABC′)(ABC') bằng aa, góc giữa hai mặt phẳng (ABC′)(ABC') và (BCC′B′)(BCC'B') bằng α\alpha với cos⁡α=123\cos \alpha=\frac{1}{2\sqrt{3}}. Thể tích khối lăng trụ ABC⋅A′B′C′ABC\cdot A'B'C' bằng mn2a3(m>1)\frac{m\sqrt{n}}{2}a^{3}(m>1). Tính m+nm+n.

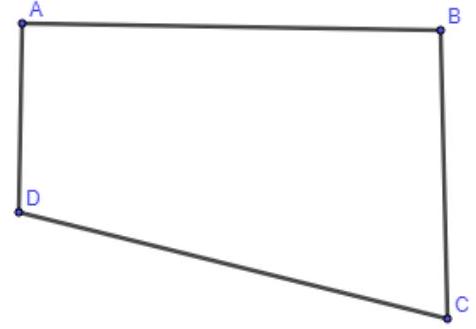
chi tiết

Câu 2. Một phần sân trường được định vị bởi các điểm A,B,C,DA, B, C, D như hình vẽ. Bước đầu, chúng được lấy "thăng bằng" để có cùng độ cao, biết ABCDABCD là hình thang vuông ở AA và BB với độ dài AB=25 mAB=25\,m, AD=15 mAD=15\,m, BC=18 mBC=18\,m. Do yêu cầu kĩ thuật, khi lát phẳng phần sân trường phải thoát nước về góc sân ở CC nên người ta lấy độ cao ở các điểm B,C,DB, C, D xuống thấp hơn so với độ cao ở AA là 10 cm10\,cm, a cma\,cm, 6 cm6\,cm tương ứng. Tính giá trị của aa.

Hình minh họa
chi tiết

Câu 3. Trong một đợt khám sức khỏe của 50 học sinh nam lớp 12, người ta được kết quả về chiều cao (đơn vị: cm) của các học sinh như bảng dưới đây.

Nhóm[160;164)[160 ; 164)[164;168)[164 ; 168)[168;172)[168 ; 172)[172;176)[172 ; 176)[176;180)[176 ; 180)
Tần số3818129n=50n=50

Độ lệch chuẩn của mẫu số liệu ghép nhóm cho ở bảng trên bằng bao nhiêu centimét (làm tròn kết quả đến hàng phần mười)?

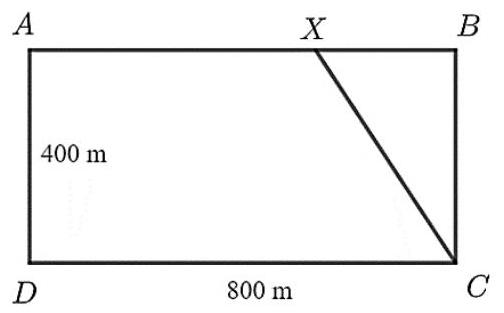
chi tiết

Câu 4. Một vận động viên thể thao hai môn phối hợp luyện tập với một bể bơi hình chữ nhật, rộng 400 m, dài 800 m. Vận động viên chạy phối hợp với bơi như sau: Xuất phát từ điểm AA, chạy đến điểm XX và bơi từ điểm XX đến điểm CC như hình bên. Hỏi nên chọn điểm XX cách AA gần bằng bao nhiêu mét để vận động viên đến CC nhanh nhất (làm tròn kết quả đến hàng đơn vị)? Biết rằng vận tốc chạy là 30 km/h30\,km/h, vận tốc bơi là 6 km/h6\,km/h.

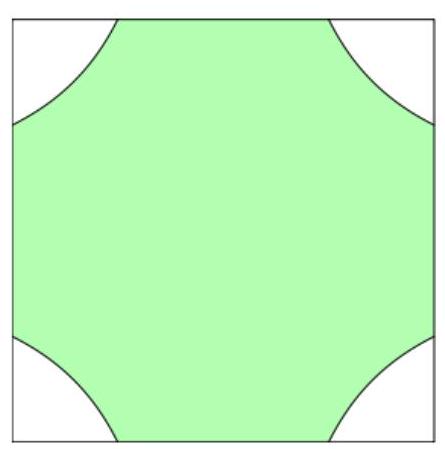
Hình minh họa
chi tiết

Câu 5. Người ta thiết kế một mẫu gạch lát nền nhà có dạng hình vuông, cạnh 4 dm. Bốn góc viên gạch màu trắng, phần ở giữa màu xanh (như hình vẽ). Đường viền của phần màu xanh bao gồm bốn đoạn thẳng nằm trên các cạnh hình vuông và bốn đường cong có tính chất: Tích khoảng cách từ một điểm bất kỳ thuộc đường cong đó đến hai trục đối xứng của viên gạch (hai đường thẳng đi qua tâm viên gạch và lần lượt song song với hai cạnh vuông góc) bằng 2 dm22\,dm^{2}. Hãy cho biết phần màu xanh có diện tích bằng bao nhiêu decimét vuông (làm tròn kết quả đến hàng phần mười)?

Hình minh họa
chi tiết

Câu 6. Dân số trung bình sơ bộ năm 2021 của tỉnh A là 1.191.782 người, tăng 1,75%1,75\% so với năm 2020. Hỏi với tốc độ tăng dân số được duy trì mức 1,75%1,75\% một năm thì đến năm bao nhiêu dân số tỉnh A lần đầu vượt 1.880.000 người.

chi tiết

---HẾT---