Đề Thi Thử Môn Toán THPT 2025 - Đề Số 19 - VuaDeThi.com

Trắc nghiệm trả lời ngắn

Câu 5. Từ hình chữ nhật $ABCD$ có chiều dài $AB=10\,cm$ và chiều rộng $BC=5\,cm$, người ta cắt bỏ miền $(R)$ được giới hạn bởi cạnh $CD$ của hình chữ nhật và hai nửa đường parabol có chung đỉnh là trung điểm của cạnh $AB$, chúng lần lượt đi qua hai đầu mút $C, D$ của hình chữ nhật đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục $AB$ để tạo nên một đồ vật làm trang trí, thể tích của vật trang trí đó bằng $a\pi\,cm^{3}$. Tìm $a$.

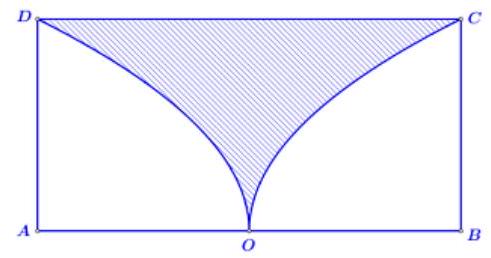
xem đáp án bên dưới

Đáp án

125

Chọn hệ trục tọa độ như hình vẽ bên thì $C(5 ; 5)$ và parabol bên phải trục $O y$ có dạng $\left(P_{1}\right): y^{2}=2 p x$.

Ta có $C \in\left(P_{1}\right) \Leftrightarrow p=\frac{5}{2}$. Suy ra $\left(P_{1}\right): y^{2}=5 x$ hay $y=\sqrt{5 x}$.

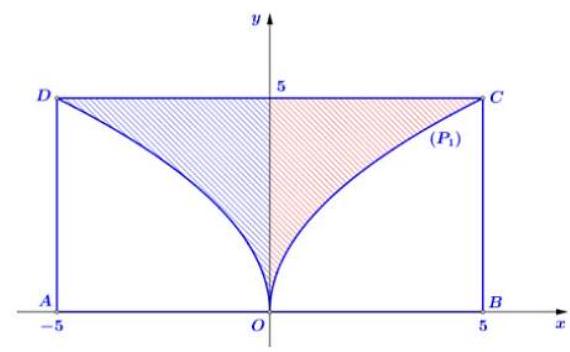
Sau khi cắt bỏ miền $(R)$ và cho phần còn lại quay quanh trục $A B$ (trục $O x$ ) ta được vật trang trí có thể tích là $V=2 \pi \int_{0}^{5}(\sqrt{5 x})^{2} \mathrm{~d} x=125 \pi\left(\mathrm{~cm}^{3}\right)$. Vậy $a=125$.