PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 3. Cô Hà thống kê lại đường kính thân gỗ của một số cây xoan đào 6 năm tuổi được trồng ở một lâm trường ở bảng sau:
| Đường kính (cm) | |||||
|---|---|---|---|---|---|
| Tần số | 5 | 20 | 18 | 7 | 3 |
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
A. 25 .
B. 30 .
C. 6 .
D. 69,8 .
Câu 7. Trong không gian , cho mặt phẳng . Vectơ nào sau đây là vectơ pháp tuyến của ?
A. .
B. .
C. .
D. .
Câu 8. Cho hình chóp có đáy là hình vuông, vuông góc với mặt phẳng đáy. Mệnh đề nào sau đây đúng?
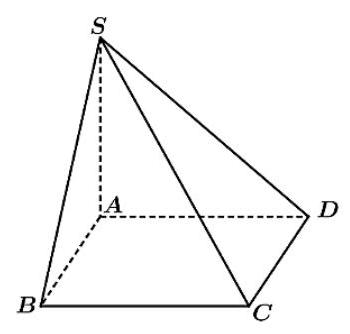
A. .
B. .
C. .
D. .
Câu 12. Cho hàm số có đồ thị như hình vẽ bên. Hàm số đồng biến trên khoảng nào trong các khoảng dưới đây?
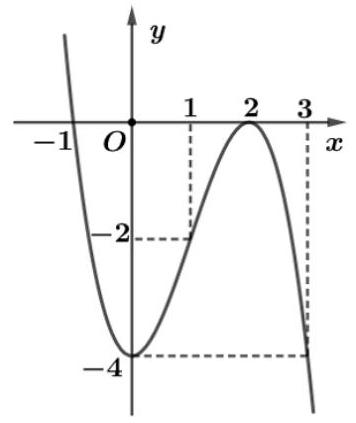
A. .
B. .
C. .
D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4.
Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số .
a) .
b) Đạo hàm của hàm số đã cho là .
c) Nghiệm của phương trình trên đoạn là .
d) Giá trị nhỏ nhất của trên đoạn là .
Câu 2. Để đảm bảo an toàn khi lưu thông trên đường, các xe ô tô khi dừng đèn đỏ phải cách nhau tối thiểu 1 m. Một ô tô đang chạy với vận tốc thì gặp ô tô đang dừng đèn đỏ nên ô tô hãm phanh và chuyển động chậm dần đều với vận tốc được biểu thị bởi công thức (đơn vị: mét/giây, thời gian tính bằng giây).

a) Thời điểm xe ô tô dừng lại là 4 giây.
b) Quãng đường (đơn vị: mét) mà ô tô đi được trong thời gian giây kể từ khi hãm phanh được tính theo công thức .
c) Từ khi bắt đầu hãm phanh đến khi dừng lại, xe ô tô đi được quãng đường 32 m.
d) Để có 2 ô tô và đạt khoảng cách an toàn khi dừng lại, thì ô tô phải hãm phanh khi cách ô tô một khoảng ít nhất là 33 m.
Câu 3. Một chiếc hộp có 80 viên bi, trong đó có 50 viên bi màu đỏ và 30 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Sau khi kiểm tra, người ta thấy có số viên bi màu đỏ đánh số và số viên bi màu vàng có đánh số, những viên bi còn lại không đánh số.
a) Số viên bi màu đỏ có đánh số là 30.
b) Số viên bi màu vàng không đánh số là 15.
c) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra có đánh số là .
d) Lấy ra ngẫu nhiên một viên bi trong hộp. Xác suất để viên bi được lấy ra không có đánh số là .
Câu 4. Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí và sẽ hạ cánh ở vị trí trên đường băng (như hình vẽ).
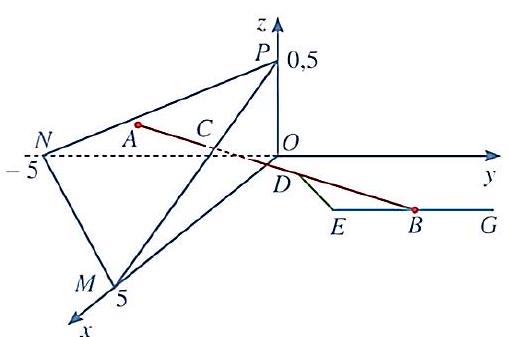
a) Đường thẳng có phương trình tham số là .
b) Khi máy bay ở vị trí thì máy bay cách mặt đất 120 m.
c) Có một lớp mây được mô phỏng bởi một mặt phẳng đi qua ba điểm , , . Vị trí mà máy bay xuyên qua đám mây để hạ cánh là .
d) Theo quy định an toàn bay, người phi công phải nhìn thấy điểm đầu của đường băng ở độ cao tối thiểu là 120 m. Nếu sau khi ra khỏi đám mây, tầm nhìn của người phi công là 900 m thì người phi công đã không đạt được quy định an toàn bay.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hình chóp có , đáy là hình chữ nhật và . Góc giữa cạnh bên và mặt đáy bằng . Khoảng cách giữa hai đường thẳng và bằng bao nhiêu?
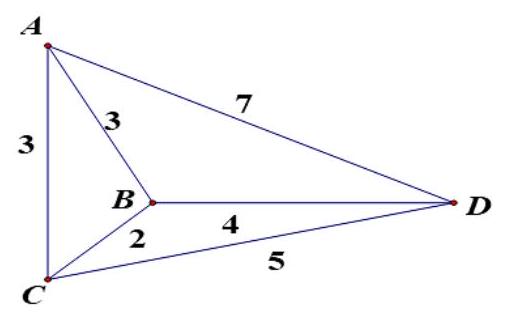
chi tiếtCâu 2. Công ty giao hàng nhanh có 4 kho hàng và . Quản lý muốn lên kế hoạch cho xe giao hàng đi qua tất cả các kho hàng để lấy hàng và quay lại kho hàng ban đầu, với điều kiện là mỗi kho hàng chỉ ghé qua một lần. Khoảng cách giữa các kho hàng (đơn vị: kilômét) được mô tả trong hình bên. Quãng đường ngắn nhất để xe giao hàng hoàn thành việc lấy hàng ở các kho và quay trở lại kho hàng ban đầu là bao nhiêu kilômét?
Câu 3. Trong không gian , một viên đạn được bắn ra từ điểm và trong 4 giây, đầu đạn đi với vận tốc không đổi, vectơ vận tốc (trên giây) là . Biết viên đạn trúng mục tiêu tại điểm , tính (viết kết quả dưới dạng số thập phân).
chi tiếtCâu 4. Một công ty sản xuất dụng cụ thể thao nhận được một đơn đặt hàng sản xuất 8000 quả bóng tennis. Công ty này sở hữu một số máy móc, mỗi máy có thể sản xuất 30 quả bóng trong một giờ. Chi phí thiết lập các máy này là 200 nghìn đồng cho mỗi máy. Khi được thiết lập, hoạt động sản xuất sẽ hoàn toàn diễn ra tự động dưới sự giám sát. Số tiền phải trả cho người giám sát là 192 nghìn đồng một giờ. Số máy móc công ty nên sử dụng là bao nhiêu để chi phí hoạt động là thấp nhất?
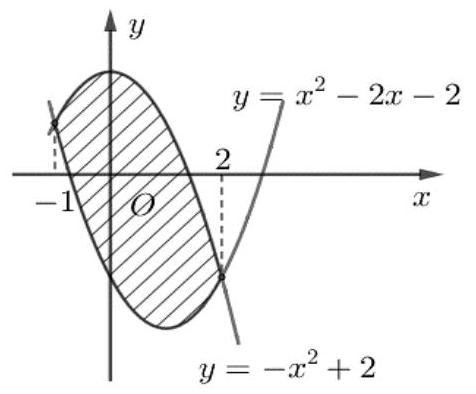
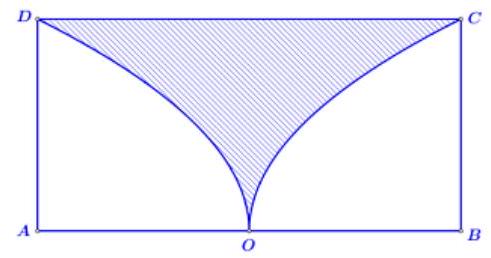
chi tiếtCâu 5. Từ hình chữ nhật có chiều dài và chiều rộng , người ta cắt bỏ miền được giới hạn bởi cạnh của hình chữ nhật và hai nửa đường parabol có chung đỉnh là trung điểm của cạnh , chúng lần lượt đi qua hai đầu mút của hình chữ nhật đó (phần tô đậm như hình vẽ). Phần còn lại cho quay quanh trục để tạo nên một đồ vật làm trang trí, thể tích của vật trang trí đó bằng . Tìm .
Câu 6. Một cặp trẻ sinh đôi có thể do cùng một trứng (sinh đôi thật), hay do hai trứng khác nhau sinh ra (sinh đôi giả). Các cặp sinh đôi thật luôn có cùng giới tính. Đối với cặp sinh đôi giả thì giới tính của mỗi đứa độc lập với nhau và có xác suất 0,5 là con trai. Thống kê cho thấy cặp sinh đôi đều là trai, cặp sinh đôi đều là gái, và cặp sinh đôi có giới tính khác nhau. Chọn ngẫu nhiên một cặp sinh đôi thì được một cặp có cùng giới tính. Tính xác suất để đó là cặp sinh đôi thật (làm tròn kết quả đến hàng phần trăm).
chi tiết---HẾT---