PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12 .
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 3. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên?
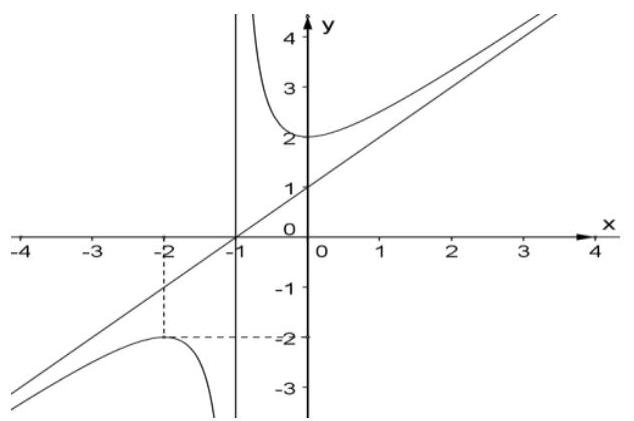
A. .
B. .
C. .
D. .
Câu 12. Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra có ít nhất 1 quyển là môn toán.
A. .
B. .
C. .
D. .
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 .
Trong mỗi ý ), b), ), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
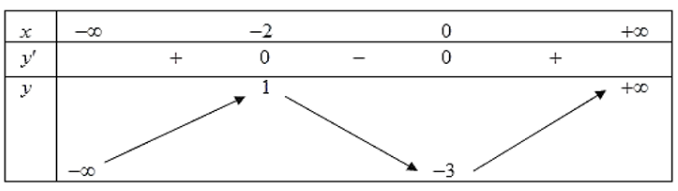
Câu 1. Cho hàm số .
a) .
b) Đạo hàm của hàm số là .
c) Một nghiệm của phương trình là .
d) Tổng các nghiệm của phương trình trong đoạn bằng .
Câu 2. Hình vẽ sau mô tả vị trí của máy bay vào thời điểm 9 giờ 30 phút. Biết các đơn vị tính theo đơn vị kilômét.
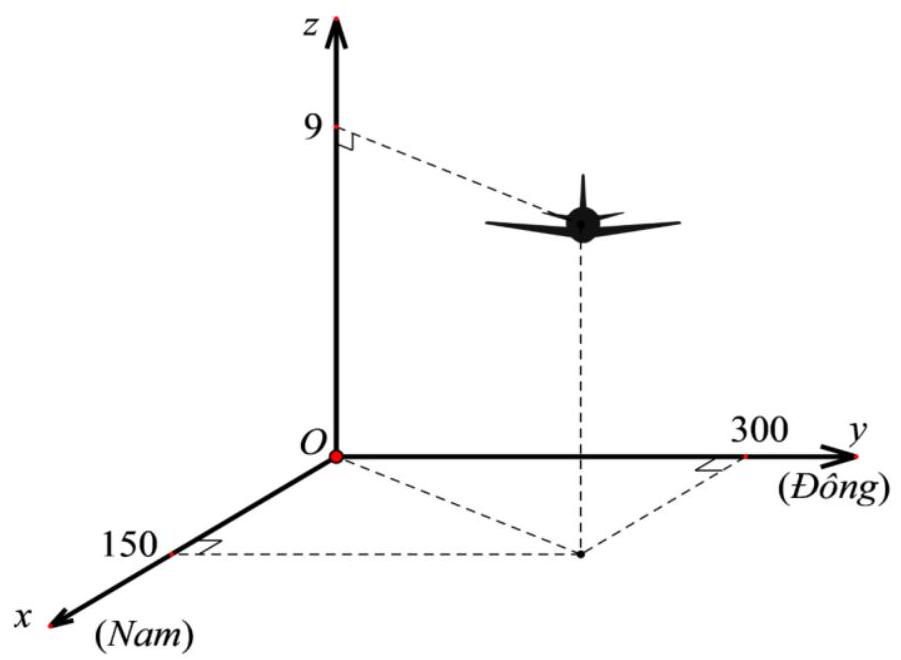
a) Máy bay đang ở độ cao 9 km .
b) Tọa độ của máy bay lúc 9 giờ 30 phút là .
c) Phi công để máy bay ở chế độ tự động và bay theo hướng đông, độ cao không đổi lúc 10 giờ 30 phút máy bay ở tọa độ . Khi đó vận tốc của máy bay là , biết vận tốc gió theo hướng đông là .
d) Giả sử vận tốc và hướng gió không đổi thì sau khi bay đến vị trí lúc 10 giờ 30 phút thì máy bay bay ngược lại (hướng Tây) với vận tốc với độ cao không đổi biết lúc đó trời lặng gió thì lúc 11 giờ máy bay cách gốc tọa độ một khoảng 723 km (làm tròn đến hàng đơn vị).
Câu 3. Một người điều khiển ô tô đang ở đường dẫn muốn nhập làn vào đường cao tốc. Khi ô tô cách điểm nhập làn 240 m , tốc độ của ô tô là . Bốn giây sau đó, ô tô bắt đầu tăng tốc với tốc độ với , trong đó là thời gian tính bằng giây kể từ khi bắt đầu tăng tốc. Biết rằng ô tô nhập làn cao tốc sau 16 giây và duy trì sự tăng tốc trong 30 giây kể từ khi bắt đầu tăng tốc.
a) Quãng đường ô tô đi được từ khi bắt đầu tăng tốc đến khi nhập làn là 208 m .
b) Giá trị của là 8 .
c) Quãng đường (đơn vị: mét) mà ô tô đi được trong thời gian giây kể từ khi tăng tốc được tính theo công thức .
d) Sau 30 giây kể từ khi tăng tốc, tốc độ của ô tô không vượt quá tốc độ tối đa cho phép là .
Câu 4. Trong một khu bảo tồn động vật hoang dã, người ta đang nghiên cứu 600 con vật, trong đó có 360 con báo đốm và 240 con sư tử. Sau khi thống kê, người ta thấy có số báo đốm đã được tiêm phòng và số sư tử đã được tiêm phòng.
a) Số con báo đốm đã được tiêm phòng là 216 con.
b) Số con sư tử chưa được tiêm phòng là 108 con.
c) Chọn ra ngẫu nhiên một con vật trong số đó. Xác suất để chọn ra được một con sư tử đã được tiêm phòng là 0,4 .
d) Chọn ra ngẫu nhiên một con vật trong số đó. Xác suất để chọn ra được một con vật chưa được tiêm phòng là 0,46 .
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .
Câu 1. Hai thành phố và cách nhau một con sông. Người ta xây dựng một cây cầu bắc qua sông biết rằng thành phố cách con sông một khoảng là 5 km và thành phố cách con sông một khoảng là 7 km (hình vẽ), biết và độ dài không đổi. Hỏi nên xây cây cầu cách thành phố bao nhiêu kilômét để đường đi từ thành phố đến thành phố là ngắn nhất, biết đi theo
, tính giá trị của biểu thức . đường (kết quả làm tròn đến hàng đơn vị).
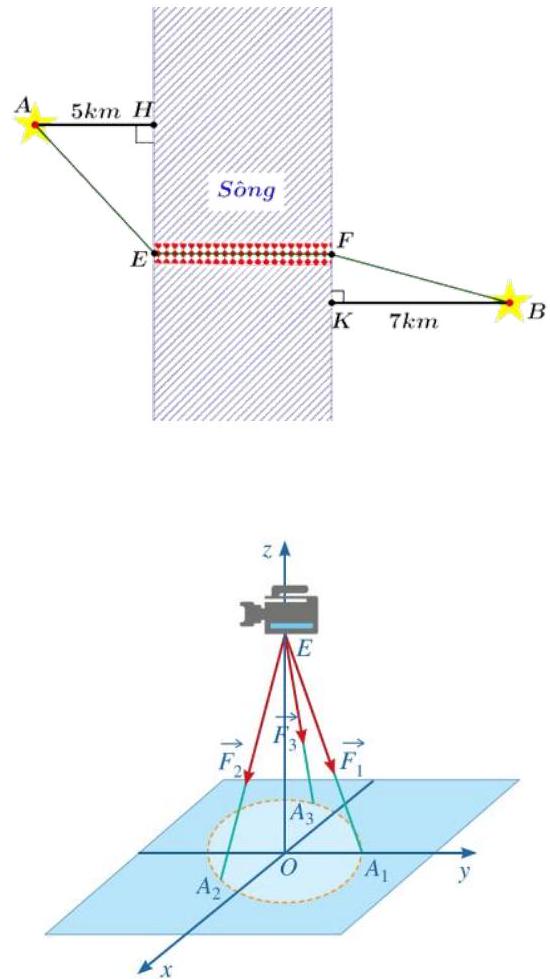
Câu 2. Một chiếc máy quay phim có trọng lượng 300 N được đặt trên một giá đỡ ba chân với điểm đặt và các điểm tiếp xúc với mặt đất của ba chân lần lượt là , , (xem hình vẽ). Giả sử
chi tiếtCâu 3. Bảng dưới đây thống kê cự li ném tạ của một vận động viên.
| Cự li | |||||
|---|---|---|---|---|---|
| Tần số | 13 | 45 | 24 | 12 | 6 |
Phương sai của mẫu số liệu ghép nhóm trên bằng bao nhiêu (kết quả làm tròn đến hàng phần trăm)?
chi tiếtCâu 4. Khu vực trung tâm một quảng trường có dạng hình tròn đường kính bằng 10 m . Người ta trang trí khu vực này bằng hai đường parabol đối xứng nhau qua , nằm trong hình tròn, đi qua các điểm và có đỉnh cách mép hình tròn 1 m . Phần giới hạn bởi 2 parabol được trồng hoa với chi phí 200 nghìn đồng 1 mét vuông, phần còn lại được lát gốm sứ với chi phí 800 nghìn đồng 1 mét vuông. Tính tổng chi phí để hoàn thành khu vực này (làm tròn kết quả đến hàng phần mười, đơn vị: triệu đồng).
chi tiếtCâu 5. Cầu Cổng Vàng (The Golden Gate Bridge) ở Mỹ. Xét hệ trục tọa độ với là bệ của chân cột trụ tại mặt nước, trục trùng với cột trụ, mặt phẳng là mặt nước và xem như trục cùng phương với cầu (xem hình vẽ). Dây cáp (xem như là một đoạn thẳng) đi qua đỉnh thuộc trục và điểm thuộc mặt phẳng , trong đó điểm là đỉnh cột trụ cách mặt nước 227 m , điểm cách mặt nước 75 m và cách trục Oz 343 m .
Giả sử ta dùng một đoạn dây nối điểm trên dây cáp và điểm trên thành cầu, biết cách mặt nước 75 m và song song với cột trụ. Tính độ dài , biết điểm cách trục Oz một khoảng bằng 230 m (làm tròn đến hàng phần chục theo đơn vị mét).

Câu 6. Một bàn cờ vua gồm ô vuông, mỗi ô có cạnh bằng 1 đơn vị. Một ô vừa là hình vuông hay hình chữ nhật, hai ô là hình chữ nhật, ... Chọn ngẫu nhiên một hình chữ nhật trên bàn cờ. Xác suất để hình được chọn là một hình vuông có cạnh lớn hơn 4 đơn vị bằng với là phân số tối giản và . Tính giá trị của biểu thức .
chi tiết---HẾT---